復習部分を追記しました。(2014/7/31)
予習
これから、『データ解析のための統計モデリング』(『緑本』と呼ばれている。*1)読書会という集まりに参加するので、その予習をメモっておきます。*2
毎回、説明が分かりやすく、応用的な知識も紹介していただけるので、私のような文系初学者にとってはありがたい勉強会です。(『緑本』自体、初学者にも分かりやすいテキストですが。)

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
- 作者: 久保拓弥
- 出版社/メーカー: 岩波書店
- 発売日: 2012/05/19
- メディア: 単行本
- 購入: 16人 クリック: 163回
- この商品を含むブログ (20件) を見る
第6章は、これまでポワソン回帰を中心に解説されてきたGLMの別のバリエーションを紹介しますというもので、二項分布を用いたロジスティック回帰と、正規分布のGLMと、ガンマ分布のGLMが解説される。
ロジスティック回帰と正規分布の間に、コラム的な位置づけなのか、「交互作用」を扱う場合の注意点と、変数間で割り算した指標を使うことの危険性が説明される。
GLMというのは、いろいろな種類の確率分布(誤差分布)やリンク関数を扱う共通のフレームワークみたいなものであり、得られたデータの性質をみながら「適切な確率分布とリンク関数を選ぶ」→「最尤法でパラメータを推定する」という手順で行う分析なので、バリエーションをたくさん知っておくとためになりますという話である。
だいたいの内容
- 二項分布は、「上限のあるカウントデータ」に使う。ある事象が「起きるか起きないか」を問題にしており、その事象が起きる確率と、サンプル数(個数の上限)が与えられた時に、そのサンプル数のうちいくつのサンプルで事象が起きるかを予測するものである。
- 二項分布をつかったGLMの定番?として、(ロジスティック関数の逆関数である)ロジット関数をリンク関数に用いたロジスティック回帰というものがある。
- ロジット関数は、事象が起きる確率をオッズ(の対数)の形に変換するものであり、このオッズを「=exp(線形予測子)」の形式で表すことで、「各変数が何倍になるとオッズが何倍になるか」を議論することができ、データの解釈がとてもしやすい場合がある。
- 交互作用項は、線形予測子内の項の積であらわされるのが一般的である。
- 交互作用項は、むやみに入れるとわけのわからないモデルになるので、無駄に使わないこと。
- ある観測変数を別の観測変数で割った指標、たとえば「単位面積あたりの」とか「単位時間あたりの」を使うのは基本的にダメ。理由は大きく二つあり、①失われる情報があるから(教科書の例だと、合成変数に一元化するからだと思う)、②割り算したあとの確率分布はとてもややこしいものになって正確に扱うのが難しくなるから。
- 割り算指標なんて使わなくても、オフセット項をモデルに入れることで、「単位面積あたりの」などという合成変数ではなく、もとの2変数(この場合は個体数と面積)のままモデルに組み込むことはできる。こういう工夫をすることで、ほとんどの場合、割り算指標なんて使う必要はなくなる。
- 正規分布とガンマ分布については、連続変数なので、確率質量の求め方と確率密度の求め方に注意する。
メモ
元のデータ対して「変数変換」を行ったり、「割り算指標」(ある変数をべつの変数で割った指標)をつくったりといった操作によって、むりやり線形回帰に持ち込もうとする人がけっこういるが、GLMの枠内で工夫することでなるべく元の変数を自然な形で扱うように、というのが本書で何度も注意を促される点で、そのために様々な分布やリンク関数の性質をしっかり勉強しましょうということだと思う。
これについては、『緑本』著者の久保先生が書かれている、
樹木・森林生態学「よく出る」誤用統計学の基本わざ
という資料のなかで、少しべつの側面も解説されていた。
本書の題6章で「ダメ」な例として紹介されている「割り算指標」は、2つの変数を1つの変数に合成してしまうことで情報量が犠牲になるというケースだった。つまり例えば、「調査地の面積」「明るさ」「発見される植物個体数」という3変数があったときに、個体数を面積で割って「密度」とし、「明るさ→密度」というモデルをつくりたくなるのだが、それはやめておけと。
上記PDFでは、それとは別に、説明変数を分母とする応答変数を設けるという明らかに無意味な分析も散見されるよという話が載っている。また、変数変換については、よくみかける「対数変換」について、対数正規分布の性質を考慮せずに対数化した変数を直線回帰すると解釈を間違えやすいよということが書かれてある。
その他のメモ。
- オッズとオッズ比が一瞬ごっちゃになる。オッズ比はある場合のオッズと別の場合のオッズの比。
- pnorm()で計算されるのが「マイナス無限大〜xまでの確率」というのは注意しようと思った。
課題(分からないことなど)
- 交互作用項が積でなければならない論理的な必然性はあるのか?分散分析や重回帰分析を習ったときにも思ったが。
- 交互作用をむやみに入れるなとのことだが、第4回の時に話題になったように、入れることにかなり必然性がある場合もけっこうあるのか?
復習
復習です(勉強会後に追記)。資料などは、↓のブログ記事にまとめられている。
第6回 「データ解析のための統計モデリング入門」 読書会に参加してきた - INPUTしたらOUTPUT!
前半の発表者の方の、「glm関数を使わなくても尤度関数を自分で書いて自力でフィッティングしてみるのもよい」というのは、たしかに理解のためにはそれもできないと、と思った。
後半の方の、色をグラデーションで分けたグラフかっこよかった。
LTも大変勉強になりました。
交互作用について
交互作用について、むやみにモデルに入れない方が良いと言われているのは「予習」のとおりなのだが、教科書でも触れられてるし発表者の方もおっしゃっていた「組み合わせがめちゃめちゃ多くなる」(組み合わせ爆発)という点は、そんなに重要な理由なのだろうか?と思った。
なんというか、それは初心者としてもすぐに分かる話なので、組み合わせ爆発の罠にはまるようなことってあるんだろうかと。多変量の場合でも交互作用に入れるのは特定の組み合わせだけの場合が多いと思うし。
むしろ本書の全体としての雰囲気から言えば、組み合わせが増えすぎて計算が大変になるということよりも、解釈が難しくなったり、どういう仮定からそのモデルが導かれたのかが自分でも分からなくなるような複雑なモデリングは、間違いのもとになるからやめなさいというぐらいの話なんじゃないだろうか。
なぜ人口密度があの形なのか
p.133で、とされているが、なぜ人口密度(という名の植物個体密度)が
になるのか?という質問(議論)があり、本をめくりながら考えていたら↑の交互作用の件を質問するのを忘れてしまった。また、そもそもその議論で他の方が言っていたこともイマイチよく聞いてなかったorz
で、なんでこれが人口密度なのかについて、私もなぜかというのはよく分からなかったのだが、久保先生の「講義のーと」でも「密度 ≥ 0 でありかつ明るさ に依存しているので」としか言われていない。
そんなに必然的な理由はないのかも知れないが、同じく久保先生の授業でのスライド(?)「何でも割り算するな!」をみると、26ページでまず「ある区画の応答変数
は平均
のポアソン分布にしたがうと仮定」とされている。つまり、明るさと面積が同じような区画で計測すると、平均
のポアソン分布にしたがって個体数が変動するとまず仮定するわけである。カウントデータなわけだし。
とりあえず、今回*3は誤差~ポアソン分布ありきで分析しますということになり、を推定するにあたっては対数リンク関数を用いることにして、しかも都合の良いことに、対数リンク関数&ポアソン分布という形を保ったまま、ポアソン分布のパラメータとなる
が「面積に比例する」という仮定もうまく線形予測子に入れてしまう方法があるのでそれを使ってみた、というぐらいの話なんだろうか?
対数リンク関数が用いられる理由が、分布をみてそれっぽいからなのか、誤差がポアソン分布する変数を解析するときの定番だからなのか、それともこの研究では経験的に明るさと個体数のあいだに指数関数的な関係が知られているという想定(理論を解説するための仮想ストーリーとして)だからなのか、はたまたべつの理由なのかというのは、私にはよく分からないので今後の課題となる。
まぁそもそも、単に計算テクニックを紹介する箇所なので、例についてあまり考え込む必要はないのかもしれないが。
割り算指標の危険性について
ところで、私のような文系初学者からすると、上述のように結局「人口密度」という概念が登場するポアソン回帰モデルで分析していることと、割り算指標としての「人口密度」を持ち出してはダメなんですよと注意されていることの関係が、イマイチ分からないわけである。何を分かっていないかを表現するのも難しいので大変もどかしいのだが。
モデル式の中に「個体数」と「面積」が別々の変数として入っている場合と、あらかじめ割り算した「密度」をモデル式に入れる場合があると思うが、それぞれに問題があるようだ。
本書では、「割り算指標」の問題点としては、①変数の合成によって情報量が失われる、②複雑な誤差分布を仮定しなければならなくなる、というデメリットがすでに解説されている。まず情報量の観点からいくと、「あらかじめ割り算方式」の場合、個体数と面積の比が同じであるような複数の調査区画のあいだの違いは無かったことにされてしまう。つまり、たとえばで10個体であった調査区画と、
で100個体の調査区画の間の違いは、ないということになる。
「別変数のまま入れる方式」の場合であれば、少なくともモデル式そのものにおいては、「密度」という概念を持ち出すことによって「面積」「個体数」という別々の変数で表されていた情報量(サンプル間の違いの特徴づけ)が失われているわけではない。「あらかじめ割り算方式」だと、情報の一部がモデリングの前にあらかじめ失われてしまう。
ただ結局、最終的に関心の対象が「密度」なのであれば、最後に情報量を削って「密度」という合成変数に縮約して解釈することになるので、似たようなものという気もするが。どうなんだろ。
結局、今回の例の場合だと、割り算指標がダメな理由は理解しづらいということが、↓のブログ記事でも書かれていた。
「データ解析のための統計モデリング入門」6.6章 割算値はなぜダメなのか? #みどりぼん - Mi manca qualche giovedi`?
むしろ、たとえば「密度ではなく個体数そのものを目的変数にしたい」という場合は(どういう場合かとかはよく分からないが)「別変数のまま入れる方式」がいいし、「ひょっとしたら面積と密度の間に何か関係があるかもしれない」と考えるなら、別変数のままいろんなモデルをためしてみたほうがいいと思うで、そういう場合であれば割り算しないことのメリットは私のような初心者にもイメージしやすいのだが、そんな低レベルな話ではないようだ。
ちなみに後者はたとえば、「調査区画が広くなると、調査員がたいへん疲れるので、途中で数える気がなくなってきて植物個体の見落としが増える」みたいなことが、データから明らかになることがあるかもしれない(てきとうに想像)。その場合、オフセット項ではなくてパラメータがついてくると思うので、内容的には別のモデルになるが。
「別変数のまま入れる方式」では情報量が失われないとしても、割り算することで「誤差分布がややこしくなる」という問題はある。これについては、今回の発表者の方も「分布はややこしくなると思われ、計算してみないと想像もつかない」と言っていて、私などは計算方法を想像することすらできない。もっと、確率について勉強しないと……。
割り算データの確率分布の問題については、『緑本』に紹介された例だけをベースに考えるよりも、久保先生の↓のスライドや、
第 60 回日本生態学会大会 自由集会 (W30) データ解析で出会う統計的問題 — その「割算」あぶなくない?
同じ集会での粕谷先生の↓のスライドをみて勉強したほうがよさそうだ。(これから勉強する、の意。)
比 連続的な量が分子にくる「割算」の場合
↓のブログ記事では、多くのケースでは「割り算の問題は気にしなくても大丈夫なのだ」ということが解説されていた。そういう場合もあるということらしい。
統計モデルに観測値と観測値の割り算値を入れても問題ない:ニュースの社会科学的な裏側
これの続きで、↓の記事で割り算値がある場合とない場合で推定の安定性を比較するシミュレーションが行われていて、私のような初心者はあまり理解が追いつかないが、将来わかるようになるといいな。
統計モデルに観測値と観測値の割り算値を入れたときのバイアス - 餡子付゛録゛
グラフを描く練習
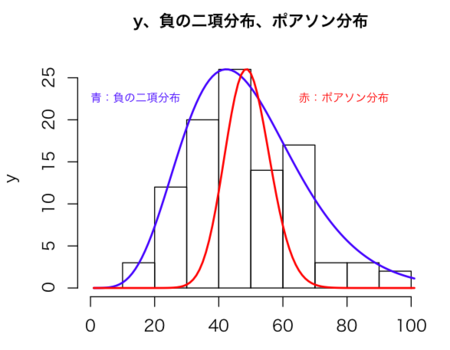
ちなみに、久保先生のサポートページからダウンロードしたデータの平均と分散をみてみると、
> d <- read.csv("http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/binomial/data4b.csv") # サポートページのデータ
>
> mean(d$y)
[1] 48.09
> var(d$y)
[1] 293.6787
という数字になっており、平均がけっこうでかく、かつ分散が平均よりずっと大きい。これって、
「使い分け」ではなく「妥当かどうか」が大事:重回帰分析&一般化線形モデル選択まわりの再まとめ
↑の記事の「早見表」に従うと、「負の二項分布」が候補になるんだろうか?
実際グラフを描いてみると、とてもよく重なります。負の二項分布でのモデリングのやり方やその意味は、まだ勉強が足りず私には分かりませんが。
hist(d$y, ylab = "y", xlab = "", main="y、負の二項分布、ポアソン分布", cex.main=1.0, xlim=c(0, 100))
par(new = TRUE)
plot(
dnbinom( # 負の二項分布をつくる
0:100,
size=((mean(d$y)^2 - mean(d$y)) / (var(d$y))), # yから計算したパラメータ(試行回数)
mu=mean(d$y), # 成功確率ではなく平均値をパラメータに指定できる
),
type="l", axes=F, ylab = "", xlab = "", col="blue", lwd=2, xlim=c(0, 100)
)par(new = TRUE)
plot(
x = seq(0:100),
dpois(0:100, mean(d$y), # 平均がyの平均に一致するポアソン分布
log = FALSE),
type = "l", axes = F, ylab = "", xlab = "", col="red", lwd=2, xlim=c(0, 100))
text(x=0, y=0.05, adj=0, labels="青:負の二項分布", cex=0.7, col="blue")
text(x=65, y=0.05, adj=0, labels="赤:ポアソン分布", cex=0.7, col="red")
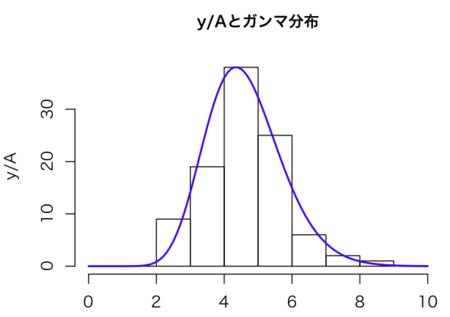
初心者なのでグラフを描く練習として、ついでににガンマ分布を重ねた図を描いてみる。
hist(d$y/d$A, ylab = "y/A", xlab = "", main="y/Aとガンマ分布", cex.main=1.0, xlim=c(0, 10), breaks=seq(0, 10, 1))
par(new = TRUE)
plot(dgamma( # y/Aの平均と分散からガンマ分布を描いてみる
seq(0, 10, by=0.1),
shape=(mean(d$y/d$A)^2/var(d$y/d$A)),
rate=(mean(d$y/d$A)/var(d$y/d$A))),
type="l", lwd=2, col="blue", axes = F, ylab = "", xlab = "")